Transposition of formula
The rearranging of formula to
calculate a variable is called the transposition
of formula or transposition. The
rules used in transposition are the same as those used in all solutions of
equations.
’the equality of an equation must be maintained’
In other words the equation must
balance. So what is done to one side of
an = must be done to the other side to maintain equality of the equation.
The principle of transposition is
to isolate one variable on one side of the = while the rest of the
variables are on the other side. It is
irrelevant which side the variables go.
One simple phrase to remember when
transposing is:
Change side = change sign
This simply means:
+ becomes -
- becomes +
x becomes ÷
÷ becomes x
√ becomes 2
You always have to be aware of the signs of a number/variable. If the number is negative it will become positive over the other side.
So moving -9 x …. For example, will become +9 ÷ over the other side of the =. This is a common mistake and if your equation doesn't work out when you calculate, look back over the steps you have taken to see if this is the problem.
Remember:
(+ +) = +
(- -) = +
(+ -) = -
Now to demonstrate how this works.
8+9=17
8=17-9
9=17-8
8+9-17=0
8 + 9 = 17
Remember how it stated that what you do to one side of the equation you must do to the other to keep it equal. Well it does not matter what you do but you must remember to do it to both sides.
So taking the equation above, you want the 8 on its own. To remove the 9 from the left side of the equation you can put a -9 into the equation. This would remove it in a mathematical sense.
8 + 9 - 9 = 17
8 + 9 - 9 = 17 - 9
8 = 17 - 9
8 + 9 - 4 = 13
8 – 8 + 9 - 4 + 4 = 13 - 8 + 4
0 0
Therefore:
9 = 13 - 8 + 4
Lets have a go at something harder.
8 x 5 = 40
To make 5 the subject, you will have to divide the left hand side by 8 to remove it. So remember to divide the right hand side too.
The 8 cancels out now.
Another way of looking at this equation is to chant the mantra ‘change side, change sign’
Moving the x5 over the = makes it a division therefore you end up with the same result.
______________________________________
Now let’s put this in letters so that you can see how rearranging formula is simpler than re-arranging numbers. Because when the formula get big it is easier to see where the letters are going rather than the numbers.
A formula for the distance moved by a body is given by:
Transpose the formula to make u the subject.
First step would be to remove the horrible fraction. This can be done by multiplying both sides by 2.
Next would be to remove the t which is multiplying the brackets as the u is in that bracket. Normally we would move the bracket first if the subject was outside it. You know that the t is multiplying and therefore division will remove it.
Now is the removal of the v from the u. To do this you need to –v on both sides.
this is your answer.
_____________________________________
A formula for kinetic energy is as follows, transpose for v.
First option would be to remove the ½ from the equation. Therefore like before, divide both sides by 2.
Now you need to separate the m from the v. Divide both sides by m.
The final step is to remove the square on the v as at the moment it is not on its own like we need. The opposite of a square number is the square root.
this is your answer.
Have a go at the following tests after practicing these equations. There are three tests for you to have a go at, Simple, Intermediate and Intense.
Practice
Transpose the following for the value in the brackets.
Transpose the following for the value in the brackets.

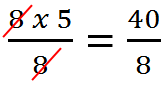














No comments:
Post a Comment