It is important to note at the beginning, all temperatures in gas law calculations must be converted to Kelvin. Therefore add 273 to any temperatures written in Celsius. If a pressure is written as a 'bar' then when calculating it needs to be converted to newtons. Take the number and add 'x10 to the power of 5' so that 5 bar would become 5 x 10 ^5.
Also it is the absolute pressure in the calculations not the gauge pressure that needs to be used.
Gas is a Fluid.
A statement that may confuse but liquids and gases have qualities that are similar. There is a page dedicated to fluids that you may read that describe the differences and similarities between gases and liquids.
This page is going to go through the 5 laws that are used to calculate and predict gases.
Charles Law
Boyles Law
Gay-Lussac Law
Combined Law
Ideal Gas Law
The above order of delivery is done to make it easier to remember and they build on each other. When calculating gas laws and working out which law to use the best method is to write down the variables available. There are always 3 of these. Pressure, Volume and Temperature. Exception is made when using the ideal gas law but then you will have many different variables available. If you write on a line
P T V
and cover the letter that you are looking for you will be given the variables that you need and they will relate to the equations that are going to be discussed now.
Charles' Law is used when calculating the volume or temperature of a gas under constant pressure. It shows the relationship between volume and temperature under constant pressure.
If a volume of gas, of fixed mass, at constant pressure expands by 1/273 of its volume at 0 deg C per deg C of rise in temperature, the relationship is:
Hence, if V = volume of gas
And T = absolute temperature of a gas
Then Charles Law may be expressed as
V ∝T Therefore V = T x C or V/T=C (constant)
If suffix 1 denotes the initial state and suffix 2 the final state of a given mass of gas, then, since V/T = a constant, we may write:
The equation must always balance, and you will need to be able to transpose the equation each time you use it.
In essence, if the temperature doubles then the volume of the gas will double.
Imagine leaving a bottle of coke in the car on a hot day. The bottle may be squeezable at the start but as the car heats up the volume of the gas within the liquid will expand in relation and eventually the bottle explodes due to the pressure being to much inside the bottle.
The same as a balloon, if the same volume of air is placed into two balloons and one place in a warm area and the other in a cold area, the warm balloon will expand and the cold one will decrease in size.
Example
The volume of a gas, of fixed mass, is inversely proportional to the pressure, provided the temperature remains constant. If absolute pressure is doubled the volume will halve, same as if the pressure is halved the volume will double as long as temperature is constant.
Imagine a plastic bottle where pressure is applied to the bottle, the volume taken up by the gas gets less and the bottle will contract.
The relationship between pressure and volume is represented in the graph below, as the volume gets bigger the pressure is decreased. as the volume decreases the pressure rises. Much like a bicycle pump if you put your finger over the end. As the pump is pushed the volume of air in the pump decreases. If the pressure is doubled the volume will halve.
Example
There is a third law that is involved but not often reflected in the universal gas law. This law only applies to ideal gases held at a constant volume allowing only the pressure and temperature to change.
If the temperature of a container is increased, the pressure increases.
If the temperature of a container is decreased, the pressure decreases.
It states that pressure is directly related to pressure, an increase in pressure in a container where the volume is kept the same will cause an increase in temperature. Same as increasing the temperature in a fixed volume container will increase the pressure.
A gas may undergo simultaneous changes in all three variables, temperature/pressure/volume . The combined gas law as it states is the accumulation of all the above in one equation. This is helpful when there are many variants available.
The main issue people will find with this equation is simply getting the transposition correct. Other than that it is as simple to use as the other laws.
When considering this equation it is possible to imagine that the final conditions are arrived at in two stages
The ideal gas law is different to the other laws that it uses a Universal Gas Constant. The universal gas constant is a physical constant used in many thermochemical equations and relationships. It is either given or can be researched for that particular element. A useful concept is that an ideal or perfect gas which obeys the laws exactly, the behavior this gas would show can be accounted for by the equation below.
In summary:
I. An ideal gas obeys the gas laws and PV = mRT exactly – no such gas exists.
II. The internal energy of the gas is entirely kinetic and depends on only its temperature.
III. The behavior of a real gas can be described in the equation if at low pressures and above temperatures at which they liquefy.
Where P,V and T are as usual and m = the mass of the gas in question. r is the universal gas constant.
The Individual Gas Constant depends on the particular gas and is related to the molecular weight of the gas. The value is independent of temperature. The Individual Gas Constant for some common gases are listed here.
|
Gas
|
J/kgK
|
|
|
Argon
|
Ar
|
208
|
|
Acetylene
|
319
|
|
|
Ammonia
|
488
|
|
|
Carbon Dioxide
|
CO2
|
188.9
|
|
Carbon Monoxide
|
CO
|
297
|
|
Carbonic acid
|
189
|
|
|
Helium
|
He
|
2077
|
|
Hydrogen
|
H2
|
4124
|
|
Methane (natural gas)
|
CH4
|
518.3
|
|
Nitrogen
|
N2
|
296.8
|
|
Oxygen
|
O2
|
259.8
|
|
Propane
|
C3H8
|
189
|
|
Sulphur Dioxide
|
SO2
|
130
|
|
Air
|
286.9
|
|
|
Water Vapour
|
461.5
|





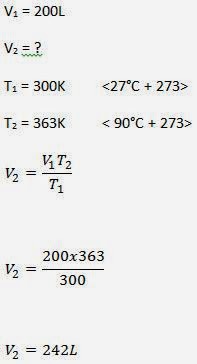










No comments:
Post a Comment