I know most people remember algebra from school and suddenly feel unhappy, nervous and scared and find this to be true:
The idea of calculating an equation with a letter in it puzzles some people but by working through the maths pages within this web program you will be able to understand how to do it and the many methods involved. A lot of the time the algebra is simply done, the letters are given known quantities but as you work through engineering many variants are represented by a letter as the quantity of that variant is always changing.
This page is going to work through many forms of algebra quickly. There will be other pages created that will develop the theory in more detail.
The Basics
If y = 7 what will the following expression be?
Because the 7 is substituted into the place of y becoming :
If z = 2. what is?
So as you can see, when here is a letter and a value for that figure it can be substituted into the equation.
These can become more complicated and with engineering maths this is more the case.
Try these to cement your understanding.
a) if y = 5 b) if p = 20 c)if m = 250 d) if x = -2
y + 7 =? p + 7 =? 2 m = ? 2 + x =?
7 - y = ? 21 + p =? m + 50 =? 6 - x =?
3 + y = ? 2 p = ? 100 - m = ? 21 - 2x =?
y - 1 = ? 5 p + 10 = ? m + 10 - 15 = ? x + x =?
Answers: (a) 12, 2, 8, 4. (b) 27, 41, 40, 110. (c) 500, 300, -150, 245. (d) 0, 8, 17, -4.
NOTE!
The more you practice maths the easier it becomes and there is no substitution for spending time learning and cheating will not help you. The answers are given so that you can check your answers to make sure you are doing it right.
Linear Equations
A linear equation sin one which can be expressed in the form
ax + b = 0
For example, each of the following equations can be rearranged into the form ax + b = 0 and solved.
Whatever is done to one side has to be done to the other side too when rearranging an equation. To solve the equation x - = 7 so that x is the subject (on its own) follow these steps.
another example
Have a go yourself.
a) 3x + 2 = 20 d) 3x + 2 = x + 8 g) 6x + 9 = 8 - 4x
b) 5x -3 =32 e) 2x - 3 = 6x +5 h) 2 - 5x = 8- 3x
c) 16 +7x =2 f) 3x +5 = 7x -8 i) 2x + 7 = 3 - 10x
The idea of calculating an equation with a letter in it puzzles some people but by working through the maths pages within this web program you will be able to understand how to do it and the many methods involved. A lot of the time the algebra is simply done, the letters are given known quantities but as you work through engineering many variants are represented by a letter as the quantity of that variant is always changing.
This page is going to work through many forms of algebra quickly. There will be other pages created that will develop the theory in more detail.
Exponents
Exponents are shorthand for repeated multiplication of the same thing by itself. Remember from your arithmetic days what this means?
That's three 2's all multiplied together:
Exponents are shorthand for repeated multiplication of the same thing by itself. Remember from your arithmetic days what this means?
That's three 2's all multiplied together:
(Because blog program will not let me use superscript I have
to use the ^ key to identify what is a small number such as the 3)
The brackets are to indicate that they are being multiplied together as explained in the mathematical functions page. Exponents are the simplest form of algebra and this is why they are the fist thing you are being taught.
The thing to remember when doing algebra is that x is a number (and any letter or shape can be used to indicate this) we just don't know which one and this is what we have to calculate.
Example
What if we stick a 5 in front of this equation?
The 5 is called a coefficient (because it's a number in front of an x ) and it's just multiplied in with the x's.)
If you were to substitute 3 in for x then you would be calculating:
The Basics
If y = 7 what will the following expression be?
y + 9 = 16
Because the 7 is substituted into the place of y becoming :
7 + 9 = 16
If z = 2. what is?
9 - z ?
9 - 2 = 7
These can become more complicated and with engineering maths this is more the case.
Try these to cement your understanding.
a) if y = 5 b) if p = 20 c)if m = 250 d) if x = -2
y + 7 =? p + 7 =? 2 m = ? 2 + x =?
7 - y = ? 21 + p =? m + 50 =? 6 - x =?
3 + y = ? 2 p = ? 100 - m = ? 21 - 2x =?
y - 1 = ? 5 p + 10 = ? m + 10 - 15 = ? x + x =?
Answers: (a) 12, 2, 8, 4. (b) 27, 41, 40, 110. (c) 500, 300, -150, 245. (d) 0, 8, 17, -4.
NOTE!
The more you practice maths the easier it becomes and there is no substitution for spending time learning and cheating will not help you. The answers are given so that you can check your answers to make sure you are doing it right.
Linear Equations
A linear equation sin one which can be expressed in the form
ax + b = 0
For example, each of the following equations can be rearranged into the form ax + b = 0 and solved.
Whatever is done to one side has to be done to the other side too when rearranging an equation. To solve the equation x - = 7 so that x is the subject (on its own) follow these steps.
x - 4 = 7
add 4 to either side to eliminate the 4 on the same side as the x
x - 4 + 4 = 7 + 4
(-4 +4 = 0 )
x + 0 = 11
x = 11
Therefore the solution is x = 11
If you are unsure of the answer you may check by putting your calculated value for x back into the original formation.
11 - 4 = 7
another example
3x - 7 = x + 3
add 7 to both sides to eliminate the 7
3x -7 +7 = x + 3 + 7
3x + 0 = x + 10
3x = x + 10
Now subtract x from both sides to eliminate x from right hand side (RHS)
3x - x = x + 10 - x
Now divide both sides by 2 so that the x is on its own
2x / 2 = 10 / 2
x = 5
Therefore the solution is x = 5
Now check you result back in the original format to make sure that both sides equal each other.
3x - 7 = x + 3
3 (5) - 7 = 5 + 3
15 - 7 = 8
8 = 8
Have a go yourself.
a) 3x + 2 = 20 d) 3x + 2 = x + 8 g) 6x + 9 = 8 - 4x
b) 5x -3 =32 e) 2x - 3 = 6x +5 h) 2 - 5x = 8- 3x
c) 16 +7x =2 f) 3x +5 = 7x -8 i) 2x + 7 = 3 - 10x
Answers: a) 6 b) 7 c) -2 d) 3 e) -2 f) -1/3 g) -1/10 h) -3 i) -1/3
Collecting Terms
Sometimes there are more than 1 algebraic term in an equation with variable values. This is when simplifying becomes useful. Imagine you have three baskets, each basket has different fruits in. apples (a) bananas (b) and pears (p).
basket 1 has 3 apples, 2 bananas and 1 pear.
basket 2 has 10 apples, 7 bananas and 6 pears.
basket 3 has 1 apple 5 bananas and 10 pears.
to put this into an algebraic form it would be related to the notations above, and include the numbers that relate to the notation.
basket 1 basket 2 basket 3
3a + 2b + 1p 10a + 7b + 6p 1a + 5b + 10p
Now to sum up the total amount of fruit in the baskets:
3a + 2b + 1p + 10a + 7b + 6p + 1a + 5b + 10p
as you can see this is untidy and mathematicians like thing tidy so what can be done is to group all the 'like' terms.
3a + 10a + 1a +2b +7b + 5b + 1p + 6p + 10p
once the like terms are together it is easy to see that the can be added (in other cases just follow the rule of the sum)
14a + 14b + 17p
It is always advised that you simplify the answer if possible in algebra.
Have a go at simplifying yourself:
a) 4x + y - 2x + 6y
b) 4y + 7p + 3k - 4y - 7k + 7p
Answers: a) 2x +7y b) 10p
Expanding the Brackets
Expanding brackets is easy once you know how so do not worry.
4 (x - 1)
If you remember from BODMAS that a bracket invites you to multiply everything inside. Therefore to expand this bracket:
4 x - 4
Now lets look at something more complicated.
4 (x+1) - 3(x-5) = 17
First is to identify each component.
4 (x+1) - 3(x-5) = 17
Expand the brackets .
4x +4 - 3x + 15 = 17
Simplify to make it easier to solve.
4x - 3x +4 + 15 = 17
x + 19 = 17
To remove the 19 from the rhs subtract from 19 both sides.
x + 19 - 19 = 17 - 19
x = -2
so the solution is x = -2
Remember you can put the solution back into the original equation to check your answer.
Now have a go on your own:
a) 2 (x - 3) + 5 (x - 1) = 3 d) 3 (x - 8) + 2 (4x - 1) = 3
b) 3( -x ) - 4 (3x - 2) = 27 e) 6 (x + 4) + (2x - 1) = 7
c) 2 (4x - 1) -3 (x - 2) = 14 f) 3 (2x + 5) - 4 (x - 3) = 0
Answers: a) 2 b) -0.266 c) 2 d) 2.64 e) -0.75 f) -13.5
Fractions
This is where algebra becomes more fun, and you will need to concentrate a little more for the first step.
consider:
Simplifying the Fraction will give
5 (x + 5) = 2 (3x + 11)
Expand the brackets like normal
5x + 25 = 6x + 22
now rearrange as previous to get all x terms on ls and other terms on the rhs
5x - 6x = 22 - 25
simplify
-x = -3
Therefore the solution is x = 3
( Because both terms are negative you are able to multiply each side by -1 which makes them a positive term. )
Another example:
cross multiply the fraction to reduce to on line
2 x 5 = 3 (x + 1)
now expand the bracket and multiply each side
10 = 3x + 3
move the x to the Lhs and the rest to the rhs
3x = 10 - 3
3x = 7
remember to remove the 3 you divide each side by 3
thus meaning the solution is x = 7/3 or 2 1/3
Now your turn:
a)
Answers: a) 7 b) -11/9 c) 16/13 d) 17/2
Multiple form equations.
So not all equations will follow what you have learnt. There will be times when linear meets fractions. Follow the next example.
Simplifying this will give
30x + 5 (x + 7) = 3 (4x -19)
now multiply out the bracket
30x + 5x + 35 = 12x - 57
move the x to the Lhs and the numbers to the rhs and do the maths
23x = -92
therefore the solution to this equations is x = - 4
Another example
Looks scary right? Well lets work through it and you will see that the principles you have learnt so far are applied and its not that much harder.
What is the common denominator? well 3 and 7 is 21 so this could be best option.
Simplifying this gives
7 ( 5x - 4) + 3 ( x + 2) = 21 (13 - x)
now multiply the brackets
35x - 28 + 3x + 6 = 273 - 21x
rearrange and do the maths
59x = 295
Therefore, after dividing both sides by 59 the solution is
x = 5
Have a go on your own.
a)
c)
Answers a) 2 b) -1 c) -1/3 d) -24/23
X to the power
This next section is going to be showing how, when cross multiplying fractions and expanding brackets the x can become a multiple of itself.
Cross multiply the brackets
now that it is on one line you can see the equation better
now expand your brackets
from this point you are able to arrange the x on one side of the equation and numbers on the other side and solve.
26x = 9
therefore the solution is x = 9 / 26
Your Turn
Basic Algebra Quiz







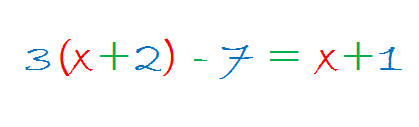
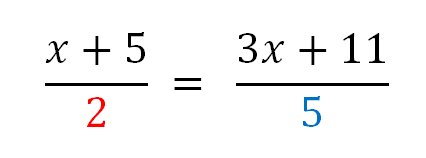






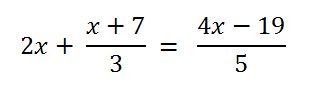

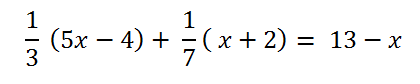







No comments:
Post a Comment